Шухов В.Г. «Механические сооружения нефтяной промышленности»

Хранение нефти и ее продуктов

Нефть и ее продукты, вырабатываемые в больших количествах, сохраняются в резервуарах или бассейнах, материал и конструк­ция которых могут быть крайне разнообразны, причем, как и во всяком промышленном сооружении, разнообразие это является результатом сочетания местных экономических условий и техни­ческих познаний строителей.

Так, если следовать по пути движения нефти от места ее до­бычи до районов потребления, то можно встретить хранилища ее в виде простых земляных ям со столбом внутри, служащим для опоры брусьев, на которых покоится настил досчатой крыши, в ви­де деревянных чанов, стянутых железными обручами, в виде обык­новенных каменных выложенных цементом бассейнов и, наконец, в виде железных резервуаров.

Мы считаем лишним говорить здесь об устройстве ям и чанов для хранения нефти, устройстве, которое очень просто, и кроме того эти типы хранилищ совершенно исчезают в рационально по­ставленном нефтяном хозяйстве.

Опыт показывает, что наиболее экономичными хранилищами как по стоимости устройства, так и в отношении эксплуатации являются железные резервуары, которые в настоящее время со­вершенно вытеснили употреблявшиеся прежде каменные бассей­ны. Последние представляют много неудобств в отношении эксплуатации, и стоимость их выше сравнительно с железными, единственное их преимущество, заключающееся в большем по­стоянстве температуры налитой жидкости, отпадает само собой при развитии перевозки нефти и ее продуктов наливом в баржах и в вагонах-цистернах.

Настоящую статью мы посвятили, главным образом, описанию железных резервуаров. Это тем более необходимо, что, насколько известно, техническая литература почти не затрагивает вопроса о рациональном устройстве железных резервуаров, служащих для хранения жидких тел.

Железные резервуары

Обыкновенный тип железного резервуара представляет собой тело цилиндрической формы с плоским днищем, покоящимся на основании, и с конической или также плоской крышей. Стены ре­зервуара образуются рядом колец, склепанных из листового же­леза; нижнее кольцо соединяется с днищем с помощью угольника. Верхнее кольцо оканчивается также угольником, который служит опорой для стропил крыши.

Рисунок 1

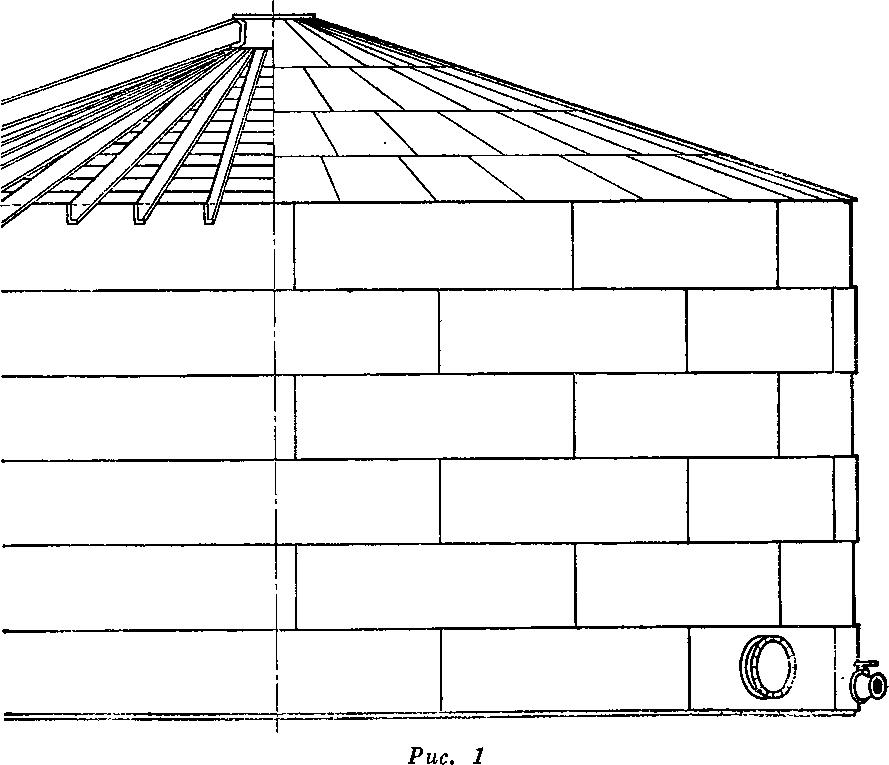
На предлагаемом рис. 1 изображен тип резервуара, наиболее распространенный в нашей нефтяной промышленности. Стропила крыши резервуара, как это видно на рис. 1, состоят из досок, рас­положенных по образующим конуса; одним концом доски упи­раются в кронштейны или башмаки, прикрепленные к верхнему угольнику, а другим — в общее чугунное кольцо, помещенное на вершине конуса. Установленные таким образом доски покрывают­ся обрешетиной, на которую ложится железо крыши. В случае значительных размеров резервуара при диаметре больше 10 саженей внутри его помещается столб, служащий для укрепления подпорок стропильных досок. В плоских крышах стропильные доски держатся с помощью подпорок, основание которых боль­шей частью укрепляется в нижний угольник, служащий для сое­динения стен с днищем.

Расчет резервуаров

Жидкость, налитая в резервуар, вызывает в материале его сте­нок напряжение, сопротивляющееся усилию разрыва, которое, как известно, пропорционально диаметру резервуара и высоте уровня налитой в него жидкости. Следовательно, наибольшее на­пряжение в материале резервуара будет вызываться в его нижнем кольце, а наименьшее — в верхнем, и если определить толщину стенок под условием достаточного сопротивления, то величина ее для верхнего кольца всякого резервуара выйдет очень незначи­тельной. С другой стороны, практика сооружения дает возможность только при известной толщине железа сделать резервуар достаточ­но жестким и достигнуть необходимой герметичности склепки и чеканки его швов; а потому независимо от усилий, действующих на резервуар, толщина железа его стенок не должна быть менее известной величины, определяемой требованиями практических условий.

Такими же практическими требованиями определяется и тол­щина железа днища резервуара, которое почти не испытывает действия внешних сил, так как оно соприкасается во всех точках с плоскостью основания, на котором устанавливается резервуар.

Кроме усилий, вызываемых давлением налитой жидкости, стены резервуара подвержены еще действию груза крыши и силе ветра, но напряжение материала, вызываемое этими силами, настолько незначительно по отношению к толщине употребляемо­го железа, что без всякого ущерба для точности вывода они могут быть не рассматриваемы.

Для крыши резервуара употребляется или обыкновенное кро­вельное железо, или же тонкое листовое, толщина которого не превышает 1/8″.

Таким образом, весь материал, употребляемый для устройства резервуара, делится: на материал, сопротивляющийся усилиям налитой жидкости, и на материал, не сопротивляющийся этим усилиям и не зависящий от них, но составляющий необходимый элемент для осуществления всего устройства; и задача расчета резервуара должна заключаться в определении его размеров при условии наименьшего веса употребленного на него железа при данной вместимости резервуара и выработанной практикой наи­меньшей толщине железа, употребляемого на дно, крышу и стены резервуара.

Рисунок 2

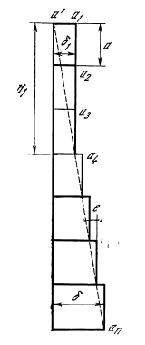
Пусть рис. 2 изображает разрез стенки резервуара плоскостью, проходящей через его ось; а1а2, а2а3, . . an-1an — а обозна­чают высоту склепанных колец листового железа, из которых состоит стенка резер­вуара.

Обозначим через Р — вместимость резер­вуара, R — его радиус и Н — высоту, ? — давление единицы высоты жидкости, Т — прочное сопротивление железа, ? = ?RH/T = HR/? — толщина нижнего кольца an-1an, ?1 — толщина железа верхнего кольца, да­ваемая практическими условиями герметич­ной склепки и чеканки, Н’ — высота, на которой от верха резервуара кольца его име­ют однообразную толщину ?1, ?n и ?m — толщина железа дна и крыши, е — разность в толщине железа двух последующих колец.

Усилие, вызываемое жидкостью в про­извольном элементе стенки резервуара, бу­дет ?Rx, где х — расстояние рассматрива­емого элемента от уровня жидкости. Необхо­димая толщина стенки для сопротивления этому усилию будет ?Rx/T; при полном нали­ве резервуара толщина его стен графически выразится прямой а’аn и наибольшее значе­ние этой толщины будет ? = ?RH/T = RH/?, где ? = Т/?. Резервуар должен быть построен таким образом, чтобы нанесенная графически толщина его колец везде перекрывала прямую линию а’аn, и размеры этой толщины дол­жны изменяться пропорционально расстоянию кольца от верха резервуара, т. е. всегда должно существовать равенство е = Ra/?. При небольшой емкости резервуаров величина ? может выйти по расчету меньше величины ?1, и потому необходимо различать два рода резервуаров: одни, в которых ?1>?, т. е. такие, где нет напряжения материала, соответствующего прочному сопротивле­нию, и другие, где ? > ?1.

Объем железа, входящего в состав резервуара, будет следующий.

Объем железа дна и крыши

q1 = ?R2 (?n + ?m) = ?R2?.

Объем железа, необходимого для сопротивления усилиям, вызываемым налитой жидкостью, или объем напряженного железа

q2 = 2?RH?/2 = ?RH?.

Объем железа, бесполезного для сопротивления

q3 = ?RH1?1

Объем избыточного железа в каждом кольце, где ? > ?1 будет ?Rae число колец такого рода в резервуаре составляет (H — H1)/а, следовательно, полный объем избыточного железа будет

q4 = ?Rae (H — Н1)/а = ?Re (H — H1), но е = Ra/?, и потому

q4 = ?R2 a/ ?(H — Н1).

Что касается объема железа, идущего на угольники, перекрыш­ки, заклепки и разные части скреплений стропил, то он может быть выражен практически вполне верно известным процентом общего количества железа, идущего на резервуар.

Таким образом, полный объем железа, идущего на устройство резервуара, будет

Q = q1 + 12 + 13 + 14 = ?R2? + ?RH? + ?RH1?1 + ?( R2a/?) H — (? R2a / a) H1

Но ? = RH/a, H1 = ?1а/R, тогда

Q = ?R2? + (?R2H2) / a + ? ?12a + (?R2a /a)H -?R a?1

Внося сюда выражение R из ?R2H = Р, получим

Q = P ?/H + P H/a + ? (?1)2 + P a/a -??R (1/?H)a?1

В резервуарах большой емкости последний член выражения Q настолько незначителен по сравнению с остальными, что его можно отбросить при определении наивыгоднейших размеров резервуара. На этом основании принимаем

Q = P ?/H + P H/a + ? (?1)2 + P a/a

Для отыскания наименьшего Q следует взять производную от его выражения по H и приравнять ее нулю. Сделав это, имеем

dQ/dH = P (-?/H2 + 1/a) = 0

откуда

H = ??a. (I)

и наименьшее количество железа, которое может быть употреблено на содержание резервуара, будет

Qmin = {2??/a + a/a} P + ? (?1)2a(II)

Примечание. Полученные таким путем уравнения (I) и (И) весьма мало отклоняются от истинного выражения высоты и веса, к которым можно прийти путем продолжительного вычисления, не отбрасывая последнего члена в уравнении (1).

В самом деле, если взять первую производную от выражения Q в уравнении (1) по II, то будем иметь

1/P dQ/dH = — ?/H2 + 1/a + 1/2 ??/P a?1/H1/2 = 0

или

H2 + 1/2 aa?1 ??/P ?H — ?a = 0

Решая это уравнение относительно H, получим

H = ??a + x2 — ?{?2x?(x2 + ?a) — x2},

x = 3?[m3/16 + ?(?a/3)3 + (m2/16)2] + 3?[m2/16 — ?(?a/3)3 + (m2/16)2]

где m = 1/2aa?1 ? ?/P .

Заметим, далее, что резервуары, для которых ? > ?1 при ?1 = 3/16″, не могут иметь вместимости меньше 20000 кубиче­ских фут. При выражении всех величин в дюймах мы будем иметь, полагая ? = 1/4″, а = 48″, что ?а = 75000 (?а/3)3 = 15 625 000000000 и m = 100 для самого невыгодного случая, т. е. для Р = 20 000. При таких цифрах трудно даже определить величину х, так как она очень близка к нулю, поэтому можно почти безошибочно положить х = 0 и тогда H = ??а.

Истинное количество железа при таком H будет

Q = {2??а + a/a ?((?/P)(1/??a))a?1}P + ? (?1)2a.

Откинутый нами в уравнении (II) член ??/P (1/4??а a?1) незначителен, что его не стоит принимать в расчет при определении веса резервуара, тем более, что при проектировании резервуара трудно избежать погрешности в распределении толщины железа последовательных колец, а такая погрешность всегда увеличивает вес резервуара.

Таким образом, для случая ? > ?1, т. е. в случае резервуаров, в стенках которых существует изменение толщины железа, про­порциональное действующим усилиям, размеры определяются из уравнения (I) и вес употребленного на них железа не должен превосходить величины, определяемой уравнением (II).

Уравнение (I) показывает, что все рационально построенные резервуары, т. е. удовлетворяющие условию min употребленного на их устройство железа, должны быть одинаковой высоты, кото­рая зависит от даваемой практикой толщины железа дна и крыши и от коэффициента прочного сопротивления, допускаемого в же­лезе, т. е. от доброкачественности последнего.

Уравнение (II) показывает, что объем железа, а следовательно, и вес его, удовлетворяющий условию min’а, пропорционален вместимости Р резервуара, причем независимо от этой вместимости в каждом резервуаре прибавляется одно и то же количество бес­полезного для сопротивления усилиям материала, выражающееся величиной ? (?1)2a.

Так, например, если два рационально устроенных резервуара, каждый вместимостью Р куб. фут. заменить одним, вместимостью 2Р, то при этом выгадывается количество материала ? (?1)2a. Зная величину этой выгоды, легко найти предел, за которым увеличение размеров резервуара теряет всякое значение, если принять во внимание практические неудобства, сопровождающие клепку, чеканку и опускание днищ резервуаров больших разме­ров.

Для отыскания наивыгоднейших размеров резервуаров, име­ющих однообразную толщину стенок по всей высоте, следует в урав­нении (I) положить ? = ?1 = const и Н = Н1 тогда имеем

Q = ?R2? + 2?RH?

или

Q = P ?/H + 2?P?H?1

Для определения minimum Q, приравниваем первую производ­ную Q по Н нулю, имеем

dQ/dH = — P ?/H2 + ?(P??1)1/?H = 0

откуда

H = 3?(P/? )(?3 /?12 ) и R = 3?(P/?)(?1/?) (III)

Следовательно, в резервуарах с однообразной толщиной сте­нок, т. е. подчиняющихся условию ?1 > RH/а, должно сущест­вовать отношение H/R = ?/?1 для того, чтобы количество употреб­ленного на них железа было наименьшее.

Эта величина наименьшего количества железа будет

Q = 3 3? [?(?1)2?] 3?P2 (IV)

Уравнение (IV) показывает, что в резервуарах, для которых ?1 > RH/а, наивыгоднейшее количество железа пропорционально

P2/3.

Предельный объем резервуаров, подлежащих последнему рас­чету, определяется следующим образом. Для предельного объ­ема должны существовать равенства ?1 = RH/a и H/R = ??1, определяя отсюда Н и R и внося их величины в выражение Р = ?R2H, будем иметь

P = ??12 ?a2/? (V)

и высота такого резервуара будет H =?a?

Таким образом, мы видим, что во всех рационально устроенных резервуарах высота их сначала возрастает пропорционально кор­ню кубическому из Р до предельного объема, выражаемого урав­нением (V), после чего, несмотря на возрастание вместимости резервуаров, высота должна оставаться постоянной. Уравнения (I),(II), (III), (IV), (V) могут решить элементарно все вопросы, относящиеся к резервуарам, если даны значения ?1 и ?.

В предыдущих выводах мы сделали предположение, что тол­щина железа нижнего кольца резервуара определяется уравне­нием ? = RH/a, где Н есть полная высота резервуара. Такое пред­положение не совсем верно, так как очевидно, что днище и его угольник влияют на сопротивление нижнего кольца и влияние их сказывается в том, что пояс наибольшего напряжения в железе отклоняется вверх, и величина этого напряжения, а следователь­но, толщина железа нижнего кольца должна определяться урав­нением ? = R (Н — х)/а, где х соответствует некоторой величине, определяющей наиболее напряженный элемент нижнего кольца. Для того чтобы определить величину я, необходимо рассмотреть условия сопротивления нижнего кольца в связи с угольником и днищем тем усилиям, которые вызываются давлением налитой жидкости.

Когда резервуар наполнен жидкостью, то радиус цилиндри­ческой поверхности его стен получает некоторое увеличение вследствие растяжения материала, подверженного усилиям. Вли­яние днища и нижнего угольника препятствует этому удлинению материала стенок, и можно сделать предположение, что дно ре­зервуара вместе с приклепанным к нему угольником, не подвергается никаким изменениям после нагрузки резервуара, так как радиальные усилия, передающиеся от стенок к дну, слишком незначительны для того, чтобы произвести радиальное же удлинение в массе металла, со­ставляющего дно и нижний уголь­ник.

Рисунок 3.

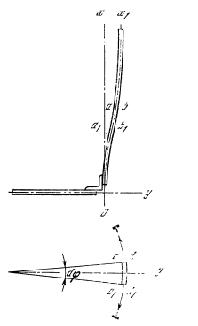
Пусть на рис. 3 обозначено: ох — средняя цилиндрическая поверхность стенок резервуара до налива в него жидкости, ох1 — видоизменение этой цилиндрической поверхности после налива жидкости в резервуар, R — радиус нижнего кольца резервуара, ? — толщина его стенок, Н — вы­сота резервуара. Возьмем за оси ко­ординат ох и оу и рассмотрим усилия, действующие на бесконечно малый элемент аaba1b1cdc1d1. Объем элемента будет ?Rd?dx, S и (S + dS) — слагаю­щие напряжения среза действующих на элемент сил параллельно оси оy, Т — слагающая напряжения разрыва действующих на элемент сил, р = (Н — х) ? — давление жидкости, где ? — вес кубической еди­ницы жидкости.

Ввиду того, что ? незначительно по отношению к R, мы можем принять, что напряжение материала одинаково во всех точках элемента.

Силы, действующие на рассматриваемый нами элемент в на­правлении оy, будут, принимая sind? = d?,

pRd?dx — dS?Rd? — T?dxd? = 0,

откуда

pR = (H — x)yR = ?8R + dS/sx +T?. (2)

Так как напряжение разрыва равняется удлинению материала, помноженному на коэффициент упругости, то в уравнении (2) Т = Ey/R, где Е — коэффициент упругости. Условие равновесия моментов дает:

момент сил упругости, развиваемых в элементе

E?3/12 Rd? 1/p — E?3/12 Rd? (1/p + d(1/p)) = — E?3/12 Rdpd1(1/p)

где р — радиус кривизны;

момент внешних сил р?Rd?dx.

Отсюда имеем, принимая, как это делается в выводах сопротив­ления материалов, 1/р = d2y/dx2,

E Rd3y/dx2 = -pR?

Дифференцируя обе части равенства и внося величину ds/dx из уравнения (2), получим

E ?3/12 R d4y/dx4 = — (H-x) yR = E y/R ?. (3)

Для интегрирования этого уравнения дадим ему следующий вид

d4y / dx4 = -12/?2R2 {(H-x) yR2/E? — y}

и, обозначив

4? 12/4?2R2 = 4?3/?R = f

будем иметь через интегрирование

y = (H-x)yR2/E? — efx(C cos fx = CI sin fx) — e-fx (CII cos fx = CIII sin fx) (4)

где С, C1, СII и СIII — четыре постоянных.

Для определения этих постоянных заметим следующее: при х = 0, у = 0 и dy/dx = 0, так как мы предполагаем, что обод днища резервуара остается неподвижным. При х = Н, т. е. в вершине резервуара, имеем также у = 0. Эти условия дадут уравнения, определяющие четыре постоянных: условие х = 0, у = 0 даст

H yR2/E? = C+CIII (a)

условие x = 0, dy/dx = 0 даст

СII-С=C + СIII + yr2/E?f (b)

условие у = 0 при х = Н дает следующее уравнение

efH (C cos fH = CI sin fH) + e-fH (CII cos fH + CIII sin fH) = 0

или

(CefH + CIIe-fH) cos fH + (CIefH + CIIIe-fH) sin fH = 0

Это уравнение распадается на два:

CefH + CIIe-fH = 0 и CIefH + CIIIe-fH = 0 (с), (d)

Заметим, что е-fH есть очень малая величина, а поэтому без особой погрешности можно принять, что CIIe-fH = 0 и CIIIe-fH = 0, а следовательно, и С = 0 и СI = 0. Эти условия дают нам из уравнения (а) СII = HyR2/E? и из уравнения (b).

CIII = yR2 / E? (H — 1/f)

Внося найденные постоянные в уравнение (1.4), будем иметь

y = (H-x)yR2/E? — e-fx (HyR2/E?)cos fx — e-fx (HyR2/E? — yR2/E?f)

или

у = yR2/E? {H-x-He-fx (cos fx = (1-1/Hf)sin fx)} .

Чтобы не усложнять вычисление, можно откинуть величину 1/fH в коэффициенте, стоящем перед sin fx, так как Н гораздо больше 1/f, тогда окончательно

у = yR2/E? {Н — x — e-fH H (cos fx + sin fx)}. (5)

Дифференцируя это уравнение по х, будем иметь

dy/dx = f yR2/E? {-1/f + 2e-fx H sin fx},

d2y/dx2 = 2f2 yR2/E? He-fx (cos fx — sin fx) и

d3y/dx3 = -4f2 R yR2/E? e-fx cos fx. (6)

Уравнения (5) и (6) вполне решают вопрос об усилиях среза и растяжения в нижнем кольце и нижнем угольнике резервуара.

Мы имели, что напряжение железа по параллели есть

Т = Ey/R = yR/? {Н — x — е-fxН (cos fx + sin fx)} (7)

и напряжение материала от срезывающих усилий

S = -E (?2/12)(d3y/dx3) = — ?/3 f3H yR2e-fx cos fx,

но

f3 = ( 4?33)(??3R3), следовательно,

S = — Hy/( 4?3)(?(R/?)e-fx )cos fx. (8)

Уравнение (7) показывает, что напряжение железа, а следо­вательно, и толщина его, соответствующая прочному сопротив­лению, в нижнем кольце будет меньше, чем мы полагали при выводе наивыгоднейших размеров резервуара, а именно

? = HR/a = HyR/T или Т = HyR/?.

В действительности при х = 0, т. е. около днища, напряжение разрыву Т = 0 и материал испытывает только напряжение среза S, которое значительно меньше величины HyR/?. Далее, начиная от днища и идя к верху, т. е. давая х постепенное приращение,

можно видеть, что величина Т будет меньше yR/?(H-x)­ до некоторого значения х = h, при котором cos fx + sin fx обращается в 0, и уже за этой точкой можно принять, что величина Т будет соответствовать силе давления жидкости. Что касается напря­жения S, то оно, как это видно из уравнения (8), быстро падает, если давать х постепенные приращения.

Вопрос должен сводиться к определению на основании урав­нения (7) с достаточной для практики точностью значения ? под условием, чтобы величина Т равнялась прочному сопротив­лению материала. Точное решение этого вопроса невозможно, так как f есть функция ?; путь же достаточно приближенного решения с помощью последовательных подстановок сопровождается слож­ными вычислениями. В самом деле, принимая ? за постоянное, определенное из ? = HR/a, мы получим, что наибольшее значе­ние Т будет при х, определенном из уравнения dT/dx = 0, что дает

sin fxe-fx = 1/2Hf. (9)

При этом d2T/dx2 = —1 + ctg fx всегда отрицательно в пределах от fx = ?/4 до fx = ?, а следовательно, Т будет max при таких значениях d2T/dx2. Решение трансцендентного уравнения (1.9) может быть получено путем последовательных подстановок.

Положим, что по данным величинам Р, ? и ? и определенным из них значениям Н, R и ? отыскано последовательными подста­новками решение уравнения (9). Пусть это решение будет х = fe, тогда наибольшее напряжение разрыву будет

Т = yR/? {Н — h — e-fhH (cos fh + sin fh)}.

Из этого уравнения можно определить, оставляя неизменным f, величину ? = ?0 под тем условием, чтобы Т равнялось прочному сопротивлению; зная ?0, можно определить f0 и, внеся обе эти величины в уравнение (7), надо будет отыскать новое значение х = h0 для получения наибольшего Т, после чего тем же путем придется отыскивать новую величину ? = ?0, и так делать до тех пор, пока не получатся два решения для ?, очень близких между собой. Для приближенного решения можно будет ограничиться второй величиной, т. е. ?0, но во всяком случае путь этот долгий.

Гораздо проще получится решение, достаточное для практи­ческих расчетов, если определить, насколько наибольшее значение Т отклоняется от того, которое соответствует Т = yR/?, где х определяется из уравнения еfxН (cos fx + sin fx) = 0.

Первое решение этого уравнения fx = 3/4 ?= приблизительно 2,3.

Целым рядом вычислений можно убедиться, что maximum Т отступает не более как на 2% от решения, полученного этим путем для резервуаров, не превосходящих 200 000 куб. фут. емкости, и потому с совершенно достаточной для практики точ­ностью можно дать формулу определения ? в следующем виде:

? = (Н — 2,2/f) R /а,

где f определяется по ? = HR/а, так что f = 4?3 ??R =( 4?3 ?a)/(R?H) и окончательно

? = (H-1,66 (R?H)/(?a))/(R/a).

Что касается толщины остальных колец, то ее следует рассчи­тывать, не принимая во внимание действие перекрышек, т. е. по формуле ? = (Н — h)R/а, где h есть расстояние рассматриваемого кольца до днища.

Влияние, оказываемое перекрышками на сопротивление ли­стов, очень незначительно; оно может быть рассмотрено тем же путем, какой был выбран нами при рассмотрении влияния днища. Уравнение в этом случае получится то же самое, т. е. (4), но для определения постоянных придется иметь дело с очень сложными уравнениями, которые могут быть решаемы только в частных слу­чаях, пользуясь незначительностью некоторых числовых коэф­фициентов.

Если наивыгоднейшие размеры резервуара определять, при­нимая во внимание значение ?, даваемое уравнением (10), то от­ступление от величины H, даваемой уравнением (I), будет настоль­ко незначительным, что его даже нельзя указать на численном примере, а потому наивыгоднейшая высота останется той же. Значение уравнения (10) выражается в том, что оно дает вес нижнего кольца в среднем на 9% меньше.

Поясним примерами употребление вышеприведенных формул. Так как при запросе на резервуары нефтепромышленники предъяв­ляют свои данные для емкости резервуаров в кубических футах или пудах нефти, кроме того, на нашем железном рынке размеры железа обозначаются в дюймах, то мы даем примеры употребле­ния формул с целью непосредственного их практического прило­жения в футах и дюймах. Построенный резервуар испытывается наливом его водой, и потому мы примем давление, производимое столбом нефти, равным давлению такого же столба воды. При­мем коэффициент прочного сопротивления Т = 300 пудов на 1 кв. дюйм.

Вес кубического дюйма воды 0,001 пуда и потому коэффициент а = 300/0,001 = 3 х 105. Толщина железа днища берется в боль­шинстве случаев в 3/16″, что совершенно достаточно для плот­ной склепки и чеканки и для полной надежности сохранения швов при опускании днищ самых больших резервуаров. Толщина же­леза крыши берется в большинстве случаев не больше 1/16». Если взять ?= 3/16″ + 1/16», то наивыгоднейшая высота Н = ??а = 274″ = 22,83′; ? = 3/16″ + 1/8″, Н = 25,6′; ? = 1/4″ + 1/8″, Н = 28′; ?1 в большинстве случаев берется равным 3/16″ И 5/32″ И редко 1/8″. Ширина листов, составляющих кольца резервуара, берется обыкновенно равной 48″.

Когда дана вместимость резервуара, то сперва следует выбрать ? и ?1, а затем, если данная вместимость больше той, которая дается уравнением (V), определить высоту по формуле (I), т. е. Н = ??а; если же данная емкость меньше величины, определяе­мой уравнением (V), высоту следует отыскивать по уравнению (III).

В случае принятого нами коэффициента прочного сопротив­ления в 300 пудов на 1 кв. дюйм, уравнение (V) примет вид Ре = 290 000 ?21, где Ре в куб. футах, ? и ?1 в дюймах. Если положить, например, ?1 = 3/16″ и ? = 1/4″, то предельный объем Pе = 20 000 куб. фут.

Вес железа, входящего в состав резервуаров, имеющих вмести­мость больше Ре, не должен превосходить того, который дается уравнением (II). Принимая вес кубического фута железа в 13,3 пуда, будем иметь, что вес резервуаров в случае прочного сопро­тивления 300 пудов должен быть П = 13,3Q = (0,046 ?? + + 0,00213) Р + 7300?21 (пудов), где Р — вместимость в куб. футах, а ? и ?1 в дюймах; так, например, при ? = 1/4″ и ?1 = 3/16″, П = 0,02513Р + 257.

К определенному таким образом весу надо прибавить 10%, которые идут на угольники, перекрышки и заклепки. Исправ­ленный такой прибавкой вес в случае ? = 1/4″ и ?1 = 3/16″ будет П = 0,028Р + 282; ? = 7/32″ и ?1 = 3/16″, П — 0,024Р + 282; ? = 7/32″ и ?1= 5/32″, П = 0,024Р + 200.

Толщина стенок нижнего кольца будет определяться по фор­муле (10), которая при а = 3 X 105 принимает вид ? = (Н — 0,003R ?H) R/а, где ?, R и H в дюймах. Найденную в этом урав­нении величину ? следует вставить в уравнение (7) для того, чтобы узнать, удовлетворяется ли условие прочного сопротивления при наибольшем Т.

Вес железа резервуаров, имеющих вместимость, меньшую Ре, определяется уравнением (IV), которое в случае ? = 1/4″ и ? = 3/16″ Дает 13,3Q = П = 4? Р2 пудов, где Р в кубических футах. К определенному по уравнению (IV) весу для небольших резер­вуаров надо прибавлять 15% на перекрышки, угольники и за­клепки.

Нам теперь остается рассмотреть условия наивыгоднейших швов и указать на некоторые детали в практике сборки и уста­новки резервуаров, что составит предмет особой главы.